Chapter 1: Discrete Geometric Quantities and Operators

import igl
import scipy as sp
import numpy as np
from meshplot import plot, subplot, interact

import os
root_folder = os.getcwd()
#root_folder = os.path.join(os.getcwd(), "tutorial")

This chapter illustrates a few discrete quantities that libigl can compute on a mesh and the libigl functions that construct popular discrete differential geometry operators. It also provides an introduction to basic drawing and coloring routines of our viewer.

Gaussian curvature

Gaussian curvature on a continuous surface is defined as the product of the principal curvatures:

$k_G = k_1 k_2.$

As an intrinsic measure, it depends on the metric and not the surface’s embedding.

Intuitively, Gaussian curvature tells how locally spherical or elliptic the surface is ( $k_G>0$ ), how locally saddle-shaped or hyperbolic the surface is ( $k_G<0$ ), or how locally cylindrical or parabolic ( $k_G=0$ ) the surface is.

In the discrete setting, one definition for a “discrete Gaussian curvature” on a triangle mesh is via a vertex’s angular deficit:

$k_G(v_i) = 2π - \sum\limits_{j\in N(i)}θ_{ij},$

where $N(i)$ are the triangles incident on vertex $i$ and $θ_{ij}$ is the angle at vertex $i$ in triangle $j$ (Meyer, 2003).

Just like the continuous analog, our discrete Gaussian curvature reveals elliptic, hyperbolic and parabolic vertices on the domain.

Let’s compute Gaussian curvature and visualize it in pseudocolor. First, calculate the curvature with libigl and then plot it in pseudocolors.

v, f = igl.read_triangle_mesh(os.path.join(root_folder, "data", "bumpy.off"))
k = igl.gaussian_curvature(v, f)
plot(v, f, k)

Next, compute the massmatrix and divide the gaussian curvature values by area to get the integral average.

m = igl.massmatrix(v, f, igl.MASSMATRIX_TYPE_VORONOI)
minv = sp.sparse.diags(1 / m.diagonal())
kn = minv.dot(k)
plot(v, f, kn)

Curvature directions

The two principal curvatures $(k_1,k_2)$ at a point on a surface measure how much the surface bends in different directions. The directions of maximum and minimum (signed) bending are called principal directions and are always orthogonal.

Mean curvature is defined as the average of principal curvatures:

$H = \frac{1}{2}(k_1 + k_2).$

One way to extract mean curvature is by examining the Laplace-Beltrami operator applied to the surface positions. The result is a so-called mean-curvature normal:

$-\Delta \mathbf{x} = H \mathbf{n}.$

It is easy to compute this on a discrete triangle mesh in libigl using the cotangent Laplace-Beltrami operator (Meyer, 2003).

l = igl.cotmatrix(v, f)
m = igl.massmatrix(v, f, igl.MASSMATRIX_TYPE_VORONOI)

minv = sp.sparse.diags(1 / m.diagonal())

hn = -minv.dot(l.dot(v))
h = np.linalg.norm(hn, axis=1)
plot(v, f, h)

Combined with the angle defect definition of discrete Gaussian curvature, one can define principal curvatures and use least squares fitting to find directions (Meyer, 2003).

Alternatively, a robust method for determining principal curvatures is via quadric fitting (Panozzo, 2010). In the neighborhood around every vertex, a best-fit quadric is found and principal curvature values and directions are analytically computed on this quadric.

v1, v2, k1, k2 = igl.principal_curvature(v, f)
h2 = 0.5 * (k1 + k2)
p = plot(v, f, h2, shading={"wireframe": False}, return_plot=True)

avg = igl.avg_edge_length(v, f) / 2.0
p.add_lines(v + v1 * avg, v - v1 * avg, shading={"line_color": "red"})
p.add_lines(v + v2 * avg, v - v2 * avg, shading={"line_color": "green"})

Gradient

Scalar functions on a surface can be discretized as a piecewise linear function with values defined at each mesh vertex:

$f(\mathbf{x}) \approx \sum\limits_{i=1}^n \phi_i(\mathbf{x})\, f_i,$

where $\phi_i$ is a piecewise linear hat function defined by the mesh so that for each triangle $\phi_i$ is the linear function which is one only at vertex $i$ and zero at the other corners.

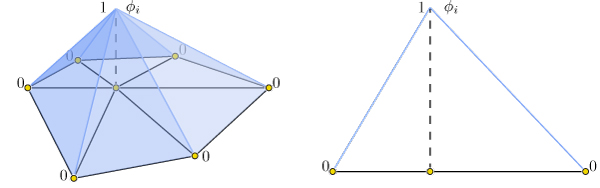
Thus gradients of such piecewise linear functions are simply sums of gradients of the hat functions:

$\nabla f(\mathbf{x}) \approx \nabla \sum\limits_{i=1}^n \phi_i(\mathbf{x})\, f_i = \sum\limits_{i=1}^n \nabla \phi_i(\mathbf{x})\, f_i.$

This reveals that the gradient is a linear function of the vector of $f_i$ values. Because the $\phi_i$ are linear in each triangle, their gradients are constant in each triangle. Thus our discrete gradient operator can be written as a matrix multiplication taking vertex values to triangle values:

$\nabla f \approx \mathbf{G}\,\mathbf{f},$

where $\mathbf{f}$ is $n\times 1$ and $\mathbf{G}$ is an $md\times n$ sparse matrix. This matrix $\mathbf{G}$ can be derived geometrically (Jacobson, 2013).

Libigl’s grad function computes $\mathbf{G}$ for triangle and tetrahedral meshes. Let’s see how this works. First load a mesh and a corresponding surface function. Next, compute the gradient operator g (#F*3 x #V) on the triangle mesh, apply it to the surface function and extract the magnitude.

v, f = igl.read_triangle_mesh(os.path.join(root_folder, "data", "cheburashka.off"))
u = igl.read_dmat(os.path.join(root_folder, "data", "cheburashka-scalar.dmat"))

g = igl.grad(v, f)
gu = g.dot(u).reshape(f.shape, order="F")

gu_mag = np.linalg.norm(gu, axis=1)
p = plot(v, f, u, shading={"wireframe":False}, return_plot=True)

max_size = igl.avg_edge_length(v, f) / np.mean(gu_mag)
bc = igl.barycenter(v, f)
bcn = bc + max_size * gu
p.add_lines(bc, bcn, shading={"line_color": "black"})

Laplacian

The discrete Laplacian is an essential geometry processing tool. Many interpretations and flavors of the Laplace and Laplace-Beltrami operator exist.

In open Euclidean space, the Laplace operator is the usual divergence of gradient (or equivalently the Laplacian of a function is the trace of its Hessian):

$\Delta f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} + \frac{\partial^2 f}{\partial z^2}.$

The Laplace-Beltrami operator generalizes this to surfaces.

When considering piecewise-linear functions on a triangle mesh, a discrete Laplacian may be derived in a variety of ways. The most popular in geometry processing is the so-called “cotangent Laplacian” $\mathbf{L}$, arising simultaneously from FEM, DEC and applying divergence theorem to vertex one-rings. As a linear operator taking vertex values to vertex values, the Laplacian $\mathbf{L}$ is a $n\times n$ matrix with elements:

$L_{ij} = \begin{cases}j \in N(i) &\cot \alpha_{ij} + \cot \beta_{ij},\\ j \notin N(i) & 0,\\ i = j & -\sum\limits_{k\neq i} L_{ik}, \end{cases}$

where $N(i)$ are the vertices adjacent to (neighboring) vertex $i$, and $\alpha_{ij},\beta_{ij}$ are the angles opposite to edge ${ij}$.

Libigl implements discrete “cotangent Laplacians” for triangles meshes and tetrahedral meshes, building both with fast geometric rules rather than “by the book” FEM construction which involves many (small) matrix inversions (Sharf, 2007).

First, load a triangle mesh and then calculate the Laplace-Beltrami operator, visualize the normals as pseudocolors.

from scipy.sparse.linalg import spsolve

v, f = igl.read_triangle_mesh(os.path.join(root_folder, "data", "cow.off"))
l = igl.cotmatrix(v, f)

n = igl.per_vertex_normals(v, f)*0.5+0.5
c = np.linalg.norm(n, axis=1)


vs = [v]
cs = [c]
for i in range(10):
    m = igl.massmatrix(v, f, igl.MASSMATRIX_TYPE_BARYCENTRIC)
    s = (m - 0.001 * l)
    b = m.dot(v)
    v = spsolve(s, m.dot(v))
    n = igl.per_vertex_normals(v, f)*0.5+0.5
    c = np.linalg.norm(n, axis=1)
    vs.append(v)
    cs.append(c)


p = subplot(vs[0], f, c, shading={"wireframe": False}, s=[1, 4, 0])
subplot(vs[3], f, c, shading={"wireframe": False}, s=[1, 4, 1], data=p)
subplot(vs[6], f, c, shading={"wireframe": False}, s=[1, 4, 2], data=p)
subplot(vs[9], f, c, shading={"wireframe": False}, s=[1, 4, 3], data=p)

# @interact(level=(0, 9))
# def mcf(level=0):
#     p.update_object(vertices=vs[level], colors=cs[level])

The operator applied to mesh vertex positions amounts to smoothing by flowing the surface along the mean curvature normal direction. Note that this is equivalent to minimizing surface area. The following example computes conformalized mean curvature flow using the cotangent Laplacian (Kazhdan, 2012)

Mass matrix

The mass matrix $\mathbf{M}$ is another $n \times n$ matrix which takes vertex values to vertex values. From an FEM point of view, it is a discretization of the inner-product: it accounts for the area around each vertex. Consequently, $\mathbf{M}$ is often a diagonal matrix, such that $M_{ii}$ is the barycentric or voronoi area around vertex $i$ in the mesh (Meyer, 2003). The inverse of this matrix is also very useful as it transforms integrated quantities into point-wise quantities, e.g.:

$\Delta f \approx \mathbf{M}^{-1} \mathbf{L} \mathbf{f}.$

In general, when encountering squared quantities integrated over the surface, the mass matrix will be used as the discretization of the inner product when sampling function values at vertices:

$\int_S x\, y\ dA \approx \mathbf{x}^T\mathbf{M}\,\mathbf{y}.$

An alternative mass matrix $\mathbf{T}$ is a $md \times md$ matrix which takes triangle vector values to triangle vector values. This matrix represents an inner-product accounting for the area associated with each triangle (i.e. the triangles true area).

Alternative construction of Laplacian

An alternative construction of the discrete cotangent Laplacian is by “squaring” the discrete gradient operator. This may be derived by applying Green’s identity (ignoring boundary conditions for the moment):

$\int_S \|\nabla f\|^2 dA = \int_S f \Delta f dA$

Or in matrix form which is immediately translatable to code:

$\mathbf{f}^T \mathbf{G}^T \mathbf{T} \mathbf{G} \mathbf{f} = \mathbf{f}^T \mathbf{M} \mathbf{M}^{-1} \mathbf{L} \mathbf{f} = \mathbf{f}^T \mathbf{L} \mathbf{f}.$

So we have that $\mathbf{L} = \mathbf{G}^T \mathbf{T} \mathbf{G}$. This also hints that we may consider $\mathbf{G}^T$ as a discrete divergence operator, since the Laplacian is the divergence of the gradient. Naturally, $\mathbf{G}^T$ is a $n \times md$ sparse matrix which takes vector values stored at triangle faces to scalar divergence values at vertices.

v, f = igl.read_triangle_mesh(os.path.join(root_folder, "data", "cow.off"))
l = igl.cotmatrix(v, f)
g = igl.grad(v, f)

d_area = igl.doublearea(v, f)
t = sp.sparse.diags(np.hstack([d_area, d_area, d_area]) * 0.5)

k = -g.T.dot(t).dot(g)
print("|k-l|: %s"%sp.sparse.linalg.norm(k-l))

|k-l|: 6.654117928693559e-13

Exact Discrete Geodesic Distances

The discrete geodesic distance between two points is the length of the shortest path between then restricted to the surface. For triangle meshes, such a path is made of a set of segments which can be either edges of the mesh or crossing a triangle.

Libigl includes a wrapper for the exact geodesic algorithm (Mitchell, 1987) developed by Danil Kirsanov (https://code.google.com/archive/p/geodesic/), exposing it through an Eigen-based API. The function

d = igl.exact_geodesic(v, f, vs, fs, vt, ft)

computes the closest geodesic distances of each vertex in vt or face in ft, from the source vertices vs or faces fs of the input mesh v, f. The output is written in the vector d, which lists first the distances for the vertices in vt, and then for the faces in ft.

v, f = igl.read_triangle_mesh(os.path.join(root_folder, "data", "bunny_small.off"))

## Select a vertex from which the distances should be calculated
vs = np.array([0])
##All vertices are the targets
vt = np.arange(v.shape[0])

d = igl.exact_geodesic(v, f, vs, vt)#, fs, ft)

strip_size = 0.02
##The function should be 1 on each integer coordinate
c = np.abs(np.sin((d / strip_size * np.pi)))
plot(v, f, c, shading={"wireframe": False})