Chapter 0

We introduce libigl with a series of self-contained examples. The purpose of each example is to showcase a feature of libigl while applying to a practical problem in geometry processing. In this chapter, we will present the basic concepts of libigl.

Libigl design principles

Before getting into the examples, we summarize the two main design principles in libigl:

1. No complex data types. We mostly use numpy or scipy matrices and vectors. This greatly favors code reusability and interoperability and forces the function authors to expose all the parameters used by the algorithm.

2. Function encapsulation. Every function is contained in a unique Python function.

Downloading Libigl

Libigl can be downloaded from PyPI:

python -m pip install libigl 

All of libigl functionality depends only on numpy and scipy. For the visualization in this tutorial we use meshplot which can be easily installed from Conda:

pip install https://github.com/skoch9/meshplot/archive/0.4.0.tar.gz 

To start using libigl (with the plots) you just need to import it together with the numpy, scipy, and meshplot.

import igl
import scipy as sp
import numpy as np
from meshplot import plot, subplot, interact

import os
root_folder = os.getcwd()

Mesh representation

Libigl uses numpy to encode vectors and matrices and scipy for sparse matrices.

A triangular mesh is encoded as a pair of matrices:

v: np.array
f: np.array

v is a #N by 3 matrix which stores the coordinates of the vertices. Each row stores the coordinate of a vertex, with its x, y and z coordinates in the first, second and third column, respectively. The matrix f stores the triangle connectivity: each line of f denotes a triangle whose 3 vertices are represented as indices pointing to rows of f.

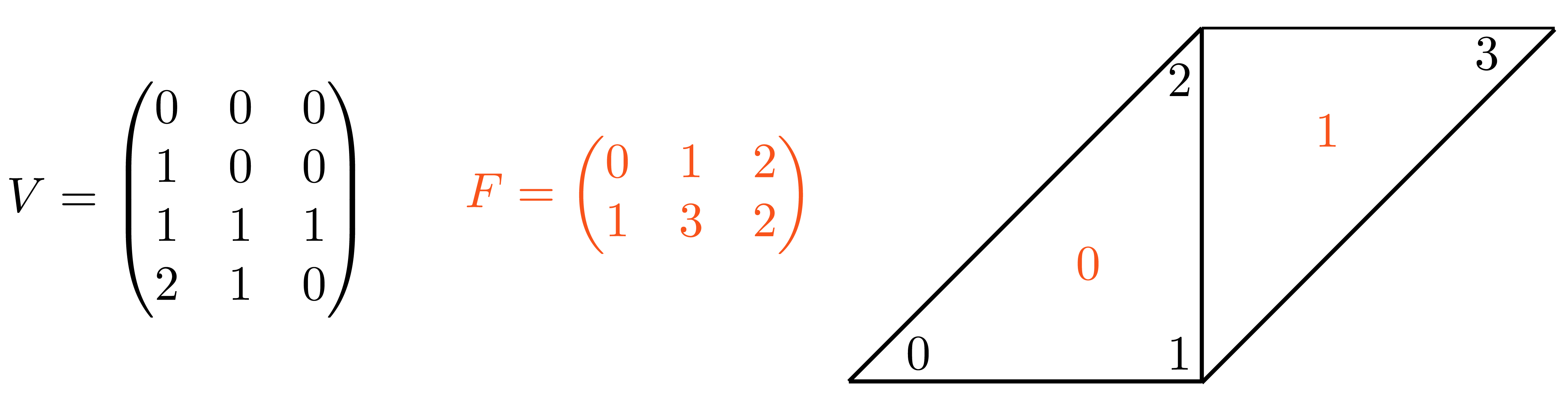
V = np.array([
    [0., 0, 0],
    [1, 0, 0],
    [1, 1, 1],
    [2, 1, 0]
])

F = np.array([
    [0, 1, 2],
    [1, 3, 2]
])

plot(V, F)

Note that the order of the vertex indices in f determines the orientation of the triangles and it should thus be consistent for the entire surface. This simple representation has many advantages:

1. It is memory efficient and cache friendly
2. The use of indices instead of pointers greatly simplifies debugging
3. The data can be trivially copied and serialized

Libigl provides input and output functions to read and write many common mesh formats. The IO functions are igl.read_* and igl.write_*.

Reading a mesh from a file requires a single libigl function call:

## Load a mesh in OFF format
v, f = igl.read_triangle_mesh(os.path.join(root_folder, "data", "bunny.off"))

## Print the vertices and faces matrices 
print("Vertices: ", len(v))
print("Faces: ", len(f))

Vertices:  3485
Faces:  6966

The function reads the mesh bumpy.off and returns the v and f matrices. Similarly, a mesh can be written to an OBJ file using:

## Save the mesh in OBJ format
ret = igl.write_triangle_mesh(os.path.join(root_folder, "data", "bunny_out.obj"), v, f)